Important Skills Needed For H2 Math: Probability and Statistics
- Zenith Education Studio

- Oct 15, 2021
- 6 min read

Probability and Statistics are arguably amongst the most important skills of the 21st century. They are in very high demand, especially in the rising sectors of machine learning, business intelligence, and economics. At the H2 A Levels, Probability and Statistics remain a fundamental portion of the total grade. In comparison to Pure Mathematics, some students may regard it to be the easier of the two to score well in. While that may be true for some students, the possibility for carelessness here is greatly magnified. In the following article, let the top Math tuition center in Singapore take you through some tips for Section B of your A Level H2 Math Paper 2!
While Pure Mathematics can get abstract and theoretical, Probability and Statistics is more quantitative and logical. The H2 A Level Math paper is divided into two. Probability and Statistics is found only in Paper 2 of the A Level Examinations under Section B. By taking up 60% of Paper 2, this means that 30% of your total A Level Grade is dedicated to Probability and Statistics! While this weightage is indeed lesser than that of Pure Math’s, it is still a sizable portion nonetheless, so it is of vital importance that we score well for this section.

Fig 1. Topics under Section B of H2 Math
Our JC Math tuition programme lists the six main topics of Section B (Fig 1). Probability stands alone at the top since it amounts to a significant portion to be learnt. Statistics comprises the next five topics. Among them, they are highly intertwined and interconnected. At the H2 A Levels, it is not uncommon for questions to integrate one or more such topics together.
Probability

Fig 2. A probability question on Permutations and Combinations
Zenith identifies that pattern recognition skills are an important asset to have when figuring out questions that deal with probability. Often, where null sets, subsets, intersections, and unions are involved, a good deal of patterns are denoted by such diagrams. That is because you may need to shade the areas which the question demands, for instance in a Venn Diagram. Other times, you may need to present your data in a Probability Distribution Table. Since the chance of each event occurring is not often constant, you will have to identify key patterns to come out with accurate probabilities, which is why Zenith stresses the importance of honing your pattern recognition skills.
Zenith’s top JC Math tuition programme identifies logical thinking as another skill that is vital for success if you’re looking to score in this chapter. One of the sub-topics under this chapter is Permutations and Combinations (Fig 2.), where it is important to analyse the possibilities demanded methodologically. Furthermore, where mutually exclusive events, independent events, and conditional probabilities are concerned, rational deduction is a must to apply each of them to their respective scenarios.
Discrete Random Variable
At the best Math tuition in Singapore, we define a discrete random variable as a countable number of possible values. As such, they best represent the number of occurrences of events or objects. Thus, this chapter most closely links to the above chapter on Probability.
It is crucial to know how to structure your answers well here. That is because the quantitative formulas of probability distributions, expectations, and variances (Fig 3.) are first introduced in this chapter. You are also required to understand how to represent a binomial distribution as a binomial random variable. In any number of ‘n’ independent trials, the outcome can only be regarded as a success or failure (hence binomial), with the probability of success for each trial, ‘p’, remaining constant. With that said, navigating your Graphing Calculator (G.C.) adeptly is absolutely essential. In particular, the binompdf and binomcdf functions to be able to find out the required probabilities which match their respective binomial variables.
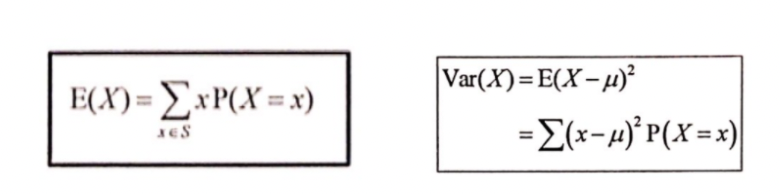
Fig 3. Expectation and Variance
Normal Distribution
Best explained as a continuous probability model, Normal Distributions differ from binomial ones in that they can take on any value in a given range. Thus, they are best suited for modeling data like height, time, mass, and distance.
At the top Math tuition center in Singapore, Zenith identifies a solid proficiency in the G.C. to be an influential factor in doing well for this chapter. Normal Distribution curves are complex, and since large data ranges are involved (Fig 4.), the aid of a calculator is inevitably required. The graphing function normalcdf allows you to evaluate probabilities lesser or bigger than a specified data value, or between two specific data values. Other times, when the probability has been explicitly given, you may instead be tasked with identifying the data point which the given probability is bounded by. In such cases, the invNorm function comes in handy. When mean and variances are unknown, then a standard distribution is assumed.

Fig 4. A normal distribution question with a high data range of 40
Sampling
At Zenith, we observe that sampling goes hand in hand with the previous chapter on Normal Distribution. For this particular chapter, the ability to make inferences is crucial. That is because sample observations and analyses are used to make inferences or predictions about a population. It is simply unfeasible to examine complete populations due to the possibility of incurring high costs. This chapter is guided by one key concept, the Central Limit Theorem which assumes that for a large number, the sampling distribution approximates a normal one for a non-normal population. If the sample data already assumes that of a normal population, then a normal distribution is used anyway. Therefore, the previously mentioned skill of being proficient with your G.C. is something that is important here as well. In many cases, the chapters on Statistics recur and overlap with one another. Being familiar with the formulas (Fig 5.) of standard deviation, variance, and mean are also absolutely necessary here. While the needed formulas for sampling may be slightly different from previous chapters, the underlying concepts remain largely unchanged. Hence, knowing when to apply the theorems to different question types is crucial.

Fig 5. Key Sampling Formulas
Hypothesis Testing
A keen eye for the bigger picture starts to develop here. In this chapter, you will be using your statistical knowledge in tandem with real-world scenarios (Fig 6.). While some terms may appear highly theoretical, like critical values, levels of significance, and p-values, there is no need for students to dive too deep into their intricacies. Rather, Hypothesis Testing follows a systematic order of steps:
Step 1: Writing down the null and alternative hypotheses
Step 2: State the level of significance
Step 3: Determine the test statistic and its distribution
Step 4: Use the G.C. to find p-value or z-value and critical value
Step 5: Reject the relevant hypotheses and arrive at a conclusion

Fig 6. A typically contextual hypothesis question
Adeptness at the G.C. aside, you should bear in mind that being able to arrive at step 5 from step 1 can only arise if you understand the demands and context of the hypothesis you are trying to prove or disprove. Only then can you decide on a test statistic to be used (step 3), or decide on whether to follow a p or z value approach (step 4). At the best Math tuition in Singapore, we develop your ability to tailor your workings to fit the requirements of hypothesis testing questions!
Correlation and Regression
Zenith pinpoints visualization skills as a much-needed trait for this chapter. Here, you will be required to break down and analyse scatter graphs, and also construct them based on the G.C. Using the product correlation coefficient, you will then have to visually determine the relationship between the different points on the graph. Also, you will have to consider the linear relationship between the data points using a least squares regression line (Fig 7.). In some cases, the A Level Math question may ask you about the reliability of your answers, or even an explanation as to why a set of data acts a certain way. Therefore, it is pivotal for you to master how to rationally interpret the relationships between data points. Sometimes, the data may not make sense at first glance, so it is ultimately up to you to try and relate it back to real-life applications. An example could be an outlier, which does not conform to the traditional layout of the scatter plot!

Fig 7. Scatter diagrams with positive (left) and negative linear correlations (right)
We hope that the above tips have been helpful! Our JC Math tuition programme seeks to foster the mathematical genius in each and every one of our students so that they will do well at the A Levels! Come and join us here, where we welcome you with open arms! You may also visit our testimonials page to find out more or contact us for a free trial today!





Comments